Foobles' Land

intro

As I mention on my front page, I am currently working on a NES demake of Yume Nikki. This game requires making random decisions at key moments, but infrequently enough that super high quality is not a concern. Random generation is not something I am particularly experienced with, which led me to searching online for existing implementations.

I ended up finding this really good resource that aggregates bunch of different 6502 PRNGs, comparing their size, speed, generation quality, etc. One that stuck out to me was White Flame's tiny and fast 8-bit PRNG. It is extremely basic, which is great! It has a 8-bit output and an 8-bit seed, because the current seed and current output are the same value! Here is White Flame's function:

        lda seed
        beq doEor
         asl
         beq noEor ;if the input was $80, skip the EOR
         bcc noEor
doEor:    eor #$1d
noEor:  sta seed

Let's step through what this is doing in words:

• Check if seed is zero.
  • If it is, then set the seed to 0x1d and stop.
• Otherwise, multiply seed by 2.
• Check if the multiplication overflowed to any non-zero value.
  • If it did, then xor seed with 0x1d.
• Save the new seed.

This isn't bad! It's a slightly modified LFSR and is, as advertised, really tiny and fast. It is almost good enough for my purposes, save for a few drawbacks that I do not like:

• When the seed is less than 128 (and nonzero), the next value is always just 2 times the previous value. Even for a simple LFSR, this is leads to EXTREMELY high correlation between outputs half of the time.
• In order to make the algorithm cover all bit patterns, the transitions into and out of 0 are special-cased. This feels slightly clumsy, and makes the algorithm slower and bigger than it needs to be.

To visualize the high correlation between outputs, here is a graph of White Flame's algorithm over many iterations:

(The algorithm for the plot is described in the page comparing all the different PRNGs, but I generated this one myself).

Here, the really obvious diagonal stripes going down-and-right represent where the PRNG is just multiplying the number by 2 successively. In the worst case, we get the sequence [1, 2, 4, 8, 16, 32, 64, 128] which is 8 consecutive values that have an extremely clear relationship.

Finally, before we continue, let's analyze this function's performance characteristics. For simplicity, let's assume that seed is a zero-page value and that the code doesn't cross any page boundaries (so branches that get taken are always 3 cycles). First, just adding the sizes of each instruction, we get that the function is 13 bytes large. Now analyzing the runtime performance characteristics, we get the following cases:

• seed == 0 (1/256): 11 cycles
• 0 < seed < 128 (127/256): 15 cycles
• seed == 128 (1/256): 13 cycles
• 128 < seed <= 255 (127/256): 16 cycles

Doing a weighted average, this gives an average time of 15.47 cycles per iteration!

Can we do better? Is there a function that improves the quality of PRNG and doesn't require special-casing for zero, while still maintaining White Flame's overall simplicity and speed? Yes! In fact, it's even better than that...

my prng

        LDA seed
        ASL A
        BCS no_eor
        EOR #$46
no_eor:
        ADC #$EB
        STA seed

Like before, let's step through what this is doing in words:

• Mulitply seed by 2.
• Check if the multiplication overflowed.
  • If it did NOT overflow, then xor seed with 0x46.
• Add 0xeb to seed with carry (i.e., if the previous multiplication overflowed, it adds 0xec instead).
• Save the new seed.

The main differences between my algorithm and White Flame's are that that there is no special-casing for 0, the xor only happens if the multiplication does NOT overflow, and there is a new unconditional add-with-carry step.

The reason I flipped the condition of the xor is to decrease the amount of correlation between consecutive values. Multiplying by 2 with no overflow is not a very "random-feeling" transformation, so in this case, we perform the xor to make the new value feel more decorrelated from the previous value. But if the multiplication does overflow, then the loss of precision acts as a different source of "randomness" instead.

Finally, the add-with-carry at the end serves to shuffle the bits just a little more, and is also a concession in order for the algorithm to cover all possible bit-patterns.

Let's look at the the graph of my function:

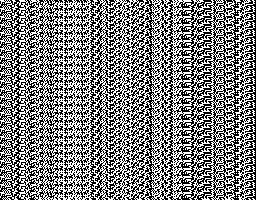
In my opinion, this looks a LOT more "random" and fuzzy than White Flame's, and the diagonal stripes are all gone too! You can still see an obvious pattern, but that is unavoidable without making the seed bigger.

Now let's look at my function's performance characteristics. Just like before, let's assume that seed is a zero-page variable and that the code doesn't cross any page boundaries. This gives us a code size of 11 bytes, which is a 2 byte saving over White Flame's! But how about speed? Here, we only have 2 cases to consider:

• 0 <= seed < 128 (128/256): 14 cycles
• 128 <= seed <= 255 (128/256): 13 cycles

Doing a weighted average, this gives an average time of 13.50 cycles, which is a an average improvement 1.97 cycles!

So all together, my algorithm is faster and smaller than White Flame's, while also generating a higher-quality sequence of 8-bit numbers. Hopefully others find this useful! Thank you for reading, and thanks to White Flame in particular for coming up with the original algorithm this is based on. Ciao!